想象一下以下的情景：

你的班主任说要选新的班长和副班长。班上有30位学生。

可以被提名当班长必须符合以下条件：

Event A - 有参加过运动会比赛（12人）

和 AND
Event B - 去年考数学80%以上（15人）

假设说你去年数学考了85%，也参加了篮球比赛。

1. 那你被选为班长的概率是多少？
   
   

当班长的概率： $$\begin{aligned} P(event) &= \frac{no. of (event)}{total\ no.\ in(Sample Space)} \\ \\ P(A) &= \frac{\cancel{12}}{\cancel{30}}
= \frac{2}{5} \\ \\ P(B) &= \frac{\bcancel{15}}{\cancel{30}} = \frac{1}{2} \end{aligned} $$

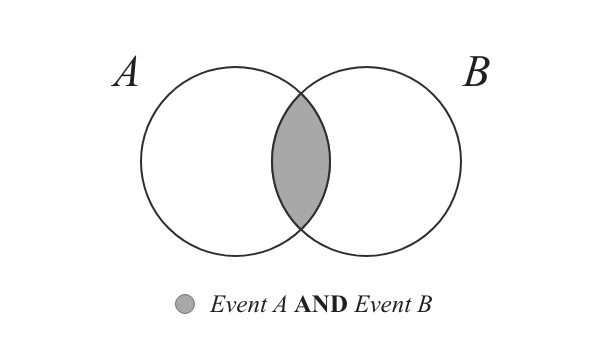(Figure 1)

现在，找到了Event A 和 Event B 各自的probability，可是我们要找的是根据Figure 1所涂黑的部分，就是两个events都要有的。这时我们就可以把
P(A) 乘 ✖️ P(B)

$$\begin{aligned} P(A\ and\ B)&= \frac{2}{5} \ \times \ \frac{1}{2} \\ &= \frac{\cancel{2}}{\cancel{10}} \\ &= \frac{1}{5} \end{aligned} $$

$$ \therefore 你被选为班长的概率是\ \frac{1}{5}\ /\ 0.2 $$

可以被提名当副班长必须符合以下条件：

Event A - 有参加过运动会比赛（12人）

或 OR

Event B - 去年考数学80%以上（15人）

2. 你被选为副班长的概率是多少？
   
   

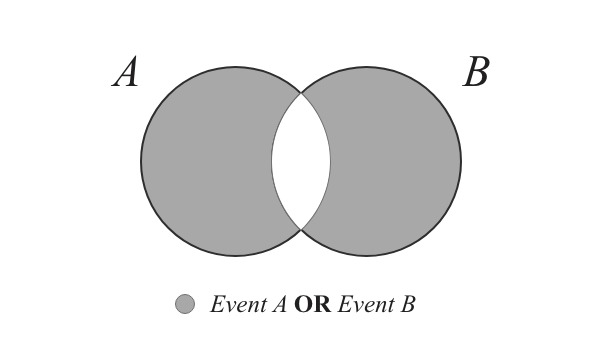(Figure 2)

这次就跟Q1不一样了，我们只要找Event A 或 Event B发生的概率，而且不能包括有两个events的交叉点。这时我们可以把
P(A) 加 ➕ P(B) 然后再减 ➖ P(A & B)

当副班长的概率：

$$\begin{aligned} P(A) + P(B) - P(A\ and\ B) &= \frac{2}{5} + \frac{1}{2} - \frac{1}{5} \\ &= \frac{4}{10} + \frac{5}{10} - \frac{2}{10} \\ &= \frac{7}{10} \end{aligned}$$

$$ \therefore 你被选为副班长的概率是\ \frac{7}{10}\ /\ 0.7 $$

所以这也表示你当副班长的机会比较高，因为只需符合其中一个条件。

Probability of Combined Events

就是计算两个事件,events 结合,combined 起来会发生的可能性。并且，两个events可以结合combined的方式有几种。

Non-mutually Exclusive Events

以上例子combined的方式称为“Non-mutually exclusive event”，就是说两个events有可能同时发生的。

Non - 非/不是
Mutual - 相互的
exclusive - 独占的
Non-mutually exclusive event - 不是相互排斥的 / 可共存

Independent Events

还有以上例子的两个Events也称为Independent Events （独立性事件），说明Event A 发生时不会影响 Event B发生的概率。

Recap

• Non-mutually Exclusive Events如果用到AND，两个events都符合 / 必须同时发生： $$P(A) \times P(B)$$

• Non-mutually Exclusive Events用到OR，只有一个event符合 / 可以其中一个发生： $$P(A) + P(B) - P(A\ and\ B)$$

Challenge Question:

How many students in the class satisfied the conditions of both Event A AND Event B?
班上有多少学生同时符合Event A 和 Event B 的条件？

要知道答案可以在FB或IG，DM @mathheroclub！：）